Computational geometry coding pattern

Distance between two points

Following are different ways to find the distance between two points on co-ordinate geometry.

Euclidean distance

Mathematical Representation:

Euclidean Distance = √[(x2 - x1)² + (y2 - y1)²]
Euclidean Distance = √[(x2 - x1)² + (y2 - y1)² + (z2 - z1)²]

Visualizing Euclidean Distance:

It’s essentially the straight-line distance between the two points.

Manhattan Distance

Mathematical Representation:

Manhattan Distance = |x2 - x1| + |y2 - y1|
Manhattan Distance = |x2 - x1| + |y2 - y1| + |z2 - z1|

Visualizing Manhattan Distance:

The Manhattan distance between two points is the shortest distance a taxi would travel to get from one point to the other, moving only along the streets and avenues.

Chebyshev distance

Mathematical Representation:

Chebyshev Distance = max(|x2 - x1|, |y2 - y1|)
Chebyshev Distance = max(|x2 - x1|, |y2 - y1|, |z2 - z1|)

Visualizing Chebyshev Distance:

Imagine a 2D grid. The Chebyshev distance between two points is the number of steps required to reach one point from the other, moving only horizontally or vertically (like a king in chess).

Note: The discrete Chebyshev distance between two spaces on a chessboard gives the minimum number of moves a king requires to move between them. This is because a king can move diagonally, so that the jumps to cover the smaller distance parallel to a row or column is effectively absorbed into the jumps covering the larger. Above are the Chebyshev distances of each square from the square f6

In a 3D space, the Chebyshev distance can be thought of as the number of steps required to move from one point to another, moving only parallel to the axes (like a king in 3D chess).

Let’s solve few problems based on distance.

1266. Minimum Time Visiting All Points

https://leetcode.com/problems/minimum-time-visiting-all-points/description/

On a 2D plane, there are n points with integer coordinates points[i] = [xi, yi]. Return the minimum time in seconds to visit all the points in the order given by points.

You can move according to these rules:

• In 1 second, you can either:
• move vertically by one unit,
• move horizontally by one unit, or
• move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in 1 second).
• You have to visit the points in the same order as they appear in the array.
• You are allowed to pass through points that appear later in the order, but these do not count as visits.

Example 1:

Input: points = [[1,1],[3,4],[-1,0]]
Output: 7
Explanation: One optimal path is [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]   
Time from [1,1] to [3,4] = 3 seconds 
Time from [3,4] to [-1,0] = 4 seconds
Total time = 7 seconds

Approach: Use Chebyshev

Since we can move either horizontal or vertical or diagonal in one unit of time therefore it is nothing but a Chebyshev distance. Following is code to implement it.

class Solution {
public:
    int minTimeToVisitAllPoints(vector<vector<int>>& points) {
        // Calculate Chebyshev distance
        int n = points.size();
        int ans = 0;
        for (int i = 1; i < n; i++) {
            vector<int> p1 = points[i - 1];
            vector<int> p2 = points[i];
            auto [x1, y1, x2, y2] = tie(p1[0], p1[1], p2[0], p2[1]);
            ans += max(abs(x1 - x2), abs(y1 - y2));
        }
        return ans;
    }
};

1057. Campus Bikes

https://leetcode.com/problems/campus-bikes/description/

On a campus represented on the X-Y plane, there are n workers and m bikes, with n <= m.

You are given an array workers of length n where workers[i] = [xi, yi] is the position of the ith worker. You are also given an array bikes of length m where bikes[j] = [xj, yj] is the position of the jth bike. All the given positions are unique.

Assign a bike to each worker. Among the available bikes and workers, we choose the (workeri, bikej) pair with the shortest Manhattan distance between each other and assign the bike to that worker.

If there are multiple (workeri, bikej) pairs with the same shortest Manhattan distance, we choose the pair with the smallest worker index. If there are multiple ways to do that, we choose the pair with the smallest bike index. Repeat this process until there are no available workers.

Return an array answer of length n, where answer[i] is the index (0-indexed) of the bike that the ith worker is assigned to.

The Manhattan distance between two points p1 and p2 is Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|.

Example 1:

Input: workers = [[0,0],[2,1]], bikes = [[1,2],[3,3]]
Output: [1,0]
Explanation: Worker 1 grabs Bike 0 as they are closest (without ties), and Worker 0 is assigned Bike 1. So the output is [1, 0].

Approach: Apply sorting

1. Prepare all possible pairs of worker and bikes
2. Sort it as per given criteria
3. allocate bike as per sorted pair

Following is code for reference.

class Solution {
public:
    vector<int> assignBikes(vector<vector<int>>& workers,
                            vector<vector<int>>& bikes) {
        int n = workers.size();
        int m = bikes.size();
        vector<tuple<int, int, int>> data;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                vector<int> worker = workers[i];
                vector<int> bike = bikes[j];
                int distance =
                    abs(worker[0] - bike[0]) + abs(worker[1] - bike[1]);
                data.push_back({distance, i, j});
            }
        }
        // Default sorting on tuple compare first, then next onwards
        sort(data.begin(), data.end());
        vector<int> ans(n, -1);
        vector<int> bikeAllocated(m, false);
        for (auto [dist, w, b] : data) {
            if (ans[w] != -1) {
                continue; // already allocated
            }
            if (bikeAllocated[b]) {
                continue; // already allocated
            }
            ans[w] = b;
            bikeAllocated[b] = true;
        }
        return ans;
    }
};

Vectors

In geometry, a vector is a quantity that has both magnitude (length) and direction.

It’s often represented visually as an arrow, where the length of the arrow represents the magnitude and the arrowhead indicates the direction.

It can be mathematically represented as below.

|v| = sqrt((x1-x2)^2 + (y1-y2)^2)
θ = arctan((y2-y1)/(x2-x1))

Can we identify starting and ending point of vector?

No. A vector is characterized by its magnitude (length) and direction, but it does not inherently have a fixed starting or ending point.

Relationship between line and vector?

Straight Line:

• Infinite extent: A line extends infinitely in both directions.
• Position: A line has a specific position in space.
• Direction: A line has a direction, but it’s not inherently associated with a magnitude.

Vector:

• Finite magnitude: A vector has a defined length or magnitude.
• Direction: A vector has a specific direction.
• Position-independent: A vector can be translated to any position in space without changing its magnitude or direction.

Although a vector can be represented as a line segment, it’s more accurate to think of it as a directed line segment.

Vector addition

Vector addition is the process of combining two or more vectors to produce a resultant vector.

There are two primary methods for visualizing and performing vector addition:

Triangle Law of Vector Addition:

• Place the tail of the second vector at the head of the first vector.
• The resultant vector is drawn from the tail of the first vector to the head of the second vector.

The formula for the magnitude |R| and direction ϕ of the resultant vector R using triangle law for the addition of vectors is given by,

|R| = √(P^2 + Q^2 + 2PQ cos θ)

ϕ = tan-1[(Q sin θ)/(P + Q cos θ)]

Parallelogram Law of Vector Addition:

• Place the tails of the two vectors together.
• Complete the parallelogram.
• The diagonal of the parallelogram, drawn from the common tail point, represents the resultant vector.

If the resultant vector R makes an angle β with the vector P, then the formulas for its magnitude and direction are:

|R| = √(P^2 + Q^2 + 2PQ cos θ)
β = tan-1[(Q sin θ)/(P + Q cos θ)]

Special Cases of Parallelogram Law of Vector Addition

When the Two Vectors are Parallel (Same Direction)

|R| = √(P^2 + Q^2 + 2PQ cos θ) = P + Q (at θ=0)
β = tan-1[(Q sin θ)/(P + Q cos θ)] = 0°

When the Two Vectors are Acting in Opposite Direction

|R| = √(P^2 + Q^2 + 2PQ cos θ) = P - Q or Q - P (at θ=180)
β = tan-1[(Q sin θ)/(P + Q cos θ)] = 0° or 180°

When the Two Vectors are Perpendicular

|R| = √(P^2 + Q^2 + 2PQ cos θ) = √(P^2 + Q^2) (at θ=90)
β = tan-1[(Q sin θ)/(P + Q cos θ)] = tan-1(Q/P)

Note: The triangle law and the parallelogram rule of vector addition are equivalent and give the same value as the resultant vector.

Vector dot product

The dot product is a mathematical operation that takes two vectors and returns a scalar (a single number).

A · B = |A| |B| cos(θ)

OR we can calculate it this way:

a · b = ax × bx + ay × by

What does this mean geometrically?

Imagine projecting one vector onto the other. The dot product gives you the product of the length of the projection and the length of the vector it’s projected onto.

Key points

• Positive Dot Product: If the angle between the vectors is acute (less than 90 degrees), the dot product is positive.
• Negative Dot Product: If the angle between the vectors is obtuse (greater than 90 degrees), the dot product is negative.
• Zero Dot Product: If the vectors are perpendicular (orthogonal), the dot product is zero.

Applications of the Dot Product in Geometry:

• Calculating the angle between two vectors: By rearranging the dot product formula, we can find the angle between two vectors:

cos(θ) = (A · B) / (|A| |B|)

• Determining orthogonality: If the dot product of two vectors is zero, they are orthogonal (perpendicular).
• Projecting one vector onto another: The dot product is used to calculate the projection of one vector onto another.
• Finding the work done by a force: In physics, the work done by a force F acting on an object that moves through a displacement d is given by the dot product:

Work = F · d

Vector Cross Product

The cross product, also known as the vector product, is a binary operation on two vectors in three-dimensional space. Unlike the dot product, which results in a scalar quantity, the cross product yields a vector that is perpendicular to both input vectors.

The magnitude (length) of the cross product equals the area of a parallelogram with vectors a and b for sides:

The cross product (blue) is:

• zero in length when vectors a and b point in the same, or opposite, direction
• reaches maximum length when vectors a and b are at right angles

We can calculate the Cross Product as below:

a × b = |a| |b| sin(θ) n

• |a| is the magnitude (length) of vector a
• |b| is the magnitude (length) of vector b
• θ is the angle between a and b
• n is the unit vector at right angles to both a and b

When a and b start at the origin point (0,0,0), the Cross Product can be calculated as below.

Right Hand Rule

With your right-hand, point your index finger along vector a, and point your middle finger along vector b: the cross product goes in the direction of your thumb.

Area of polygon

A polygon can be categorized as a regular or an irregular polygon based on the length of its sides. Thus, this differentiation also brings a difference in the calculation of the area of polygons.

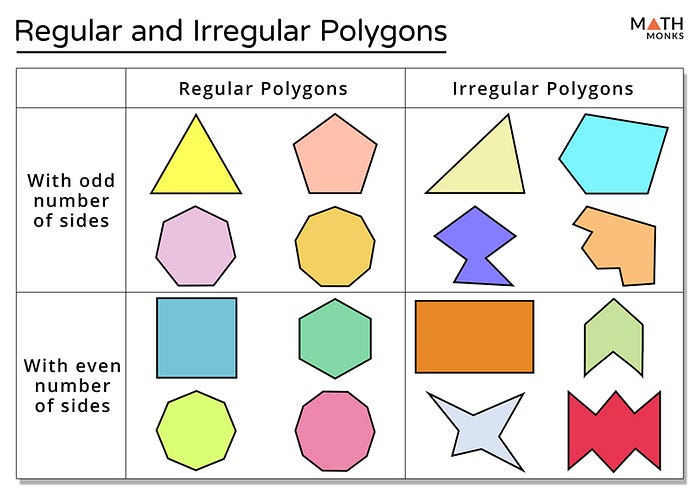
Regular polygon

A regular polygon is a two-dimensional shape having all sides of equal length and all interior angles of equal measure.

Sum of internal angle = (n-2)*180 degree

Central angle: 360/n degree

Apothem of a Regular Polygon:

Radius of a polygon

Area of regular polygon

• Area of triangle = (1/2) × base × height

Heron’s formula for triangle which is, Area = √s(s−a)(s−b)(s−c), where s = Perimeter/2 = (a + b + c)/2, a, b, and c are the length of its sides.

• Area of rectangle = length × width
• Area of parallelogram = base × height
• Area of trapezium = (1/2) × (sum of lengths of its parallel sides or bases) × height
• Area of rhombus = (1/2) × (product of diagonals)

Note: In order to calculate the area of a polygon, it must be first known whether the given polygon is a regular polygon or an irregular polygon.

Irregular Polygon

An irregular polygon, also known as non-regular polygon is a shape that does not have all sides of equal length and all angles of equal measure. Thus any polygon that is not regular is an irregular polygon.

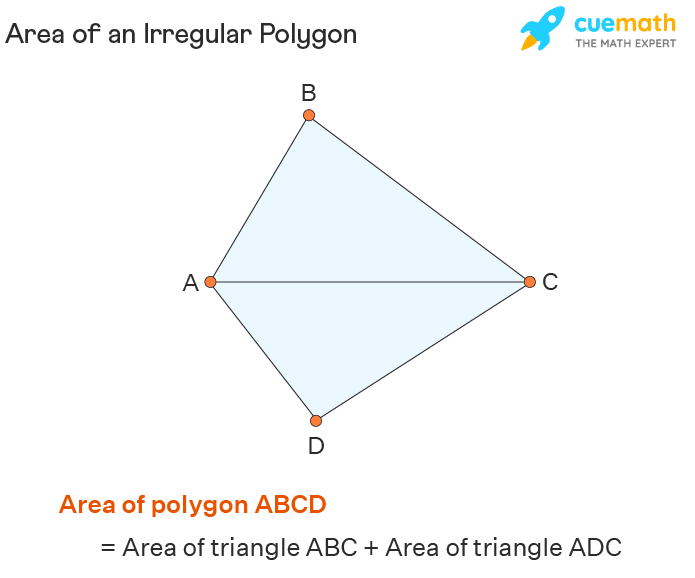
Area of Irregular Polygons

In order to calculate the area of irregular polygons, we split the irregular polygon into a set of regular polygons such that the formulas for their areas are known. Consider the example given below.

Area of Polygons with Coordinates

The area of polygons with coordinates can be found using the following steps:

• Step 1: First we find the distance between all the points using the distance formula, D = √(x2−x1)^2+(y2−y1)^2
• Step 2: Once, the dimensions of the polygons are known find whether the given polygon is a regular polygon or not.
• Step 3: If the polygon is a regular polygon we use the formula, area of regular polygon = (number of sides × length of one side × apothem)/2, where the length of apothem is given as the (length of one side)/(2 ×(tan(180°/number of sides))). If the polygon is an irregular polygon, it is to be divided into several regular polygons to find the area.

The Shoelace Formula for Area calculation for both regular or irregular polygon

Given a polygon with vertices (x₁, y₁), (x₂, y₂), …, (xn, yn), the area can be calculated using the following formula:

Area = 1/2 * |(x₁y₂ + x₂y₃ + ... + xn-1yn + xny₁) - (y₁x₂ + y₂x₃ + ... + yn-1xn + ynx₁)|

The Shoelace Theorem gets its name because if one lists the coordinates in a column,

and marks the pairs of coordinates to be multiplied,

Form of a summation

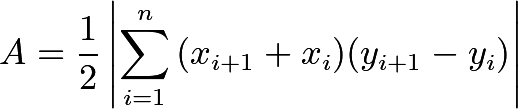
Form of determinants

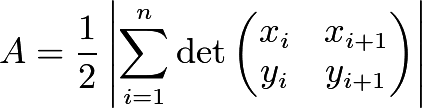
Note here that xn+1=x1 and yn+1=y1.

Let’s solve few leetcode problems.

Note: Order of (xi,yi) matters. If you swap the order then then it will give incorrect result. Except for triangle as no matter what, it will only makes one polygon.

1232. Check If It Is a Straight Line

https://leetcode.com/problems/check-if-it-is-a-straight-line/description/

You are given an array coordinates, coordinates[i] = [x, y], where [x, y] represents the coordinate of a point. Check if these points make a straight line in the XY plane.

Approach #1(Doesn’t work): Find the area of polygon using Shoelace formula

We can think to apply Shoelace formula to calculate the area of polygon made by given co-ordinates and if area is 0 then straight line otherwise not.

class Solution {
public:
    bool checkStraightLine(vector<vector<int>>& coordinates) {
        int n = coordinates.size();
        int sum = 0;
        for (int i = 0; i < n; i++) {
            vector<int> a = coordinates[i];
            vector<int> b = coordinates[(i + 1) % n];
            auto [x1, y1, x2, y2] = tie(a[0], a[1], b[0], b[1]);
            int det = (x1 * y2 - x2 * y1);
            sum += det;
        }
        double area = sum / 2.0;
        return area == 0;
    }
};

But this approach has flaw. Shoelace formula only works if the co-ordinates of each points are given in order such that it can make a single polygon.

If we mixed the order then it might make more than one polygon therefore result is not correct.

Test case for [[1,1],[2,2],[2,1],[3,2]] fails as it will make following polygon.

But if we change the order then it makes following [[1,1],[2,2],[3,2],[2,1]]

Approach #2: Use three points to build Triangle to calculate area

We can take three consecutive points to build the triangle. If any of the triangle area is non zero then we can claim that not a straight line.

How to calculate area for triangle?

Since order doesn’t matter for triangle therefore we can use Shoelace formula to calculate area.

Following is code for reference.

class Solution {
public:
    bool checkStraightLine(vector<vector<int>>& coordinates) {
        int n = coordinates.size();
        for (int i = 0; i < n - 2; i++) {
            vector<int> a = coordinates[i];
            vector<int> b = coordinates[i + 1];
            vector<int> c = coordinates[i + 2];
            auto [x1, y1, x2, y2, x3, y3] =
                tie(a[0], a[1], b[0], b[1], c[0], c[1]);
            double area =
                (x1 * y2 - y1 * x2 + x2 * y3 - y2 * x3 + x3 * y1 - y3 * x1) /
                2.0;
            if (area != 0) {
                return false;
            }
        }
        return true;
    }
};

Happy learning :-)